【Neetcode中英字幕】Advanced Algorithms

高级算法

讲师：neetcode.io

双语IT资源独家Neetcode付费课程，独家中英文字幕，配套资料齐全！

用不到1/10的价格，即可享受同样的高品质课程，且可以完全拥有，随时随地都可以任意观看和分享。

Kadane算法

Kadane 算法是一种贪婪/动态编程算法，可用于数组问题，将时间复杂度降至�(�)(n O(�)。它用于计算在特定位置结束的子数组的最大和。

动机

假设我们得到了以下问题：

问：找出总和最大的非空子数组。

这道题目要求我们在数组中找出一组相邻值的最大和。然后要求我们返回该总和。

如果我们暂时不考虑卡达内算法，蛮干的方法就是遍历每一个子数组并计算总和，同时跟踪最大总和。这样做是可行的，但会有大量重复工作。外 for 循环每迭代一次，内循环就做一次线性工作。这使得复杂度为�(n2) O(n 2)。

def bruteForce(nums):
    maxSum = nums[0]

    for i in range(len(nums)):
        curSum = 0
        for j in range(i, len(nums)):
            curSum += nums[j]
            maxSum = max(maxSum, curSum)
    return maxSum

复制

我们可以做得更好。

卡丹算法告诉我们，有一种方法只需对数组进行一次传递，就能计算出最大和，从而将复杂度降至线性时间。让我们看看如何做到这一点。

由于我们正在寻找最大的和，所以最好避免负数，因为我们知道这与问题的要求相矛盾。负数只会使我们的和变小。卡丹算法在数组上运行一个 for 循环，在每次迭代开始时，如果当前总和为负数，就会将当前总和重置为零。这样，我们就能确保一次通过，并在线性时间内解决问题。这就是代码和可视化的效果。请记住，这里的关键是，如果我们遇到的子数组的和为负数，我们就丢弃它，只要它的和为正数，我们就继续考虑它。

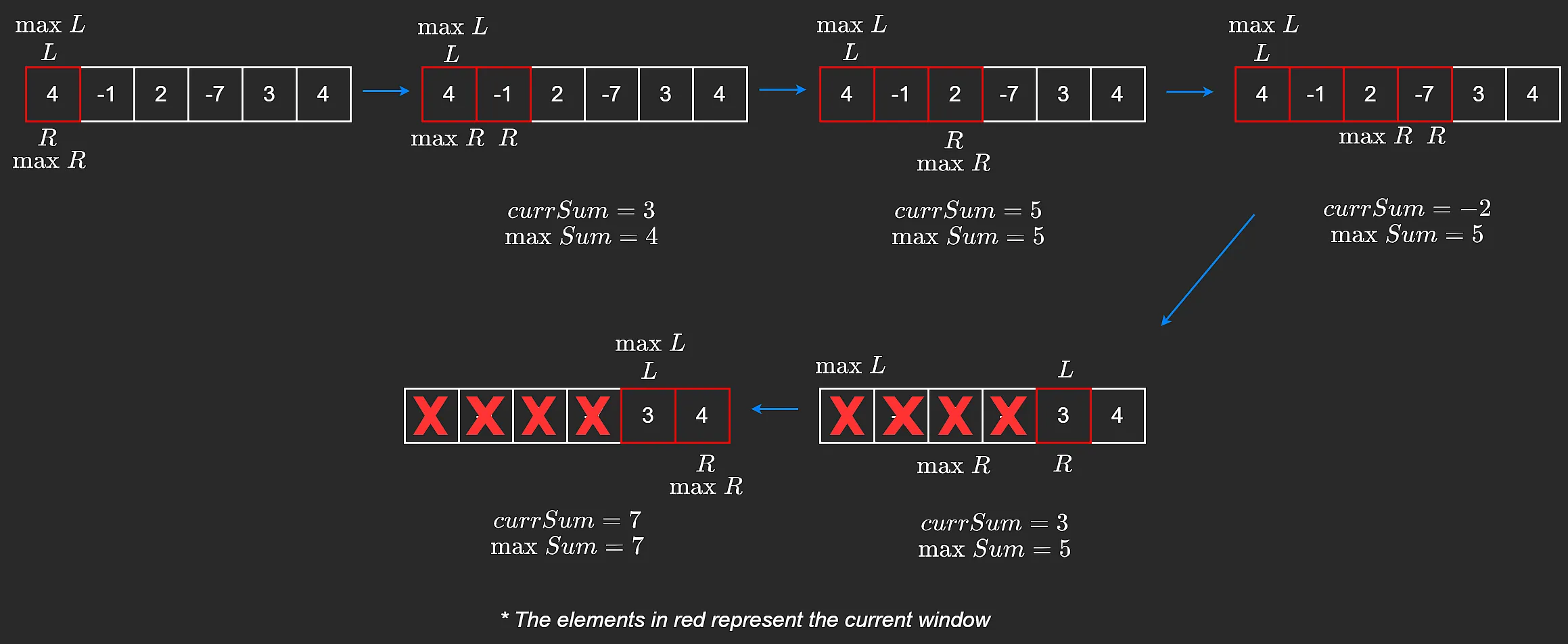
子数组指数组中连续的部分。

时间复杂性

由于我们只进行一次传递，因此时间复杂度降为�(�)nO(�)。下一章将详细讨论这个问题。

结束语

接下来，让我们正式了解一下滑动窗口技术。滑动窗口技术有两种变体，即固定滑动窗口和可变大小滑动窗口，这两种技术都适用于不同类型的问题。